Для решения систем нелинейных уравнений в среде программирования MATLAB используется процедура fsolve, входящая в пакет расширения Optimization Toolbox. Для вызова справки по этой процедуре можно воспользоваться командой help fsolve , введеной из командной строки.

Процедура fsolve решает уравнения и системы уравнений следующего вида:.

Приведем примеры уравнений и систем уравнений, которые можно решить этой процедурой:

Рассмотрим случай определения нулей функции одного переменного

fun = inline('sin(4*x)');

0.7854 3.9270

Первой строкой мы в режиме командной строки определили функцию , которая имеет имя fun. И во второй строке вызвали fsolve.

Рассмотрим подробней формат вызова fsolve.

fun – вызов функции, определенной процедурой inline,

[1 4] – решение будет найдено возле точки 1 и возле точки 4,

optimset('Display',уff') – отключить вывод на экран сообщения о результатах оптимизации.

Теперь решим эту же задачу, когда исследуемая функция является файл-функцией.

s=sin(4*x);

В активном каталоге у нас должен находиться файл myfun.m, который мы создали в редакторе MATLAB. Формат вызова fsolve или из другого m-файла (скрипт-файла) будет следующим:

x=fsolve(@myfyn,[1 4],optimset('Display','on'))

0.7854 3.9270

Теперь решим похожую задачу , возле точек 1.57 и 4.71.

Для этого определим файл-функцию myfyn1.m.

function s=myfyn1(x,c)

s=sin(4*x)-c;

Формат вызова будет следующим:

1.7017 4.8433

Рассмотрим более сложную задачу – определение точек пересечения двух линий.

Задача сводится к решению системы уравнений:

Необходимо подготовить файл-функцию для этой системы уравнений. Преобразованная система уравнений для составления файл-функции будет такой: . После такой подготовки составляем в редакторе MATLAB файл-функцию следующего вида:

function f=myfyn2(x)

f(1)=x(1)^2+x(2)^2-4^2;

f(2)=3*x(1)+x(2)-1;

Вызов процедуры fsolve со следующими параметрами:

-0.9610 3.8829

Вторая точка пересечения:

1.5610 -3.6829

Единственный недостаток процедуры fsolve видится в том, что невозможно получить все решения системы уравнений сразу. Вариант решения зависит от начальной точки итерационного процесса.

Решим при помощи процедуры fsolve следующую задачу: найти линию пересечения сферы и параболоида вращения . При решении задач такого типа, в большинстве случаев, трудоемкость и успех решения зависят от удачно выбранной параметризации. Данная формулировка задачи позволяет работать непосредственно с координатами . Исключить координату и в цикле, при фиксированном , искать значение . Но при этом возникает двойственность решения и потребуются дополнительные усилия, чтобы корректно решить эту проблему. Произведем перепараметризацию этих поверхностей:

.

На первый взгляд параметры и обозначают одно и тоже – угол с осью абцисс в плоскости , но не надо забывать, что параметры и относятся к сферической системе координат, а параметры и к цилиндрической. Конечно, если бы мы решали аналитически, приравняв параметры и , нашли значение и сказали бы, что решением является окружность радиуса на высоте . Об этом можно рассуждать достаточно долго и не в рамках наших материалов. А нам необходимо составить файл-функцию решения этой задачи, для передачи ее в процедуру fsolve.

f(3)=5*cos(p(1))-p(3)^2;

Теперь составим файл-функцию, в которой будет вызвана процедура fsolve, найдено решение и выведены все геометрические фигуры на один график.

plot3(X,Y,Z,'bo-');

После этого остается вызвать эту файл-функцию из командной строки или из другого скрипт-файла.

myfyn4

Таким образом, наша функция myfyn4 построила сферу, параболоид и линию их пересечения. Следует отметить, что массштаб по координатным осям разный, поэтому сфера выглядит как эллипсоид. Все параметры графика регулируются либо программно, либо в интерактивном режиме в среде программирования MATLAB. Можно отрегулировать выводимый диапазон значений, цвет, толщину линий и так далее.

При помощи процедуры fsolve решить следующие задачи:

1. Найти точку пересечения сферы радиуса 5 с центром в начале координат и прямой, заданной вектором n(1;2;3) и проходящей через точку А(0;0;3). Получить все решения.

2. Найти точку пересечения трех поверхностей: сферы радиуса 5 с центром в начале координат, параболоида и плоскости .

3. Построить линию пересечения эллипсоида и плоскости .

4. Решить систему уравнений: .

5. При каких значениях система уравнений имеет решения.

6. Дано семейство прямых . Найти значения параметра такого, что соответствующая прямая составляет с осью абцисс угол .

7. При помощи процедуры fsolve найти точку экстремума функции .

8. Даны две окружности: и . Необходимо построить общую касательную.

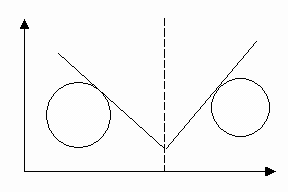
Даны две окружности: и . Определить положение касательных к окружностям таких, угол между касательными равен , а бисектрисса угла перпендикулярна оси абцисс.

10. Из точки пространства А(5;5;5) опустить перпеникуляр на поверхность, заданную уравнением .

11. Решить систему уравнений . Найти все решения.

12. Решить систему уравнений . Найти все решения.

13. Решить систему уравнений . Найти все решения.

14. Решить систему уравнений . Найти все решения.

15. Задача, при корректном решении которой возможно получить "автомат". Имеется каркас точек. Производится интерполяция составной поверхностью из порций поверхности по Кунсу. Построить коническую поверхность, касающейся интерполируемой. Вершина конуса известна. Входные данные для программы: каркас точек пространства, вершина конуса. Выходные данные: массив точек, принадлежащий и конусу, и интерполируемой поверхности. Рассмотреть возможность определения ситуаций, когда решение невозможно.