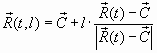 , где
, где
Построение
конических поверхностей в MATLAB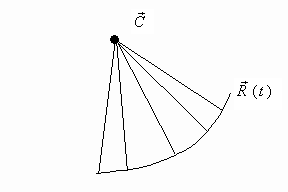
Как известно
из курса
геометрии коническую
поверхность можно
определить, задав
ее вершину
и направляющую
(рис. 1). Как
один из
вариантов описания
конической поверхности
в аналитическом
виде можно
предложить такой:
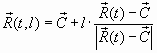 , где
, где ![]() -
направляющая,
-
направляющая, ![]() -
вершина. Способов
задания конической
поверхности множество,
но указанный
выше способ
параметризации подходит
для любого.
-
вершина. Способов
задания конической
поверхности множество,
но указанный
выше способ
параметризации подходит
для любого.
Рассмотрим еще
одно аналитическое
описание конической
поверхности. На
этот раз
правильного конуса
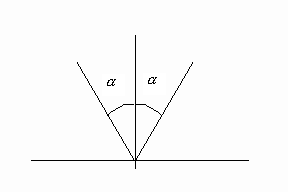
с углом
раствора ![]() и
с вершиной
в начале
координат (рис.
2):
и
с вершиной
в начале
координат (рис.
2): ![]() .
.
Такой конус проще всего описать и визуализировать в MATLAB.
y=-10:0.2:10; [X,Y]=meshgrid(x,y);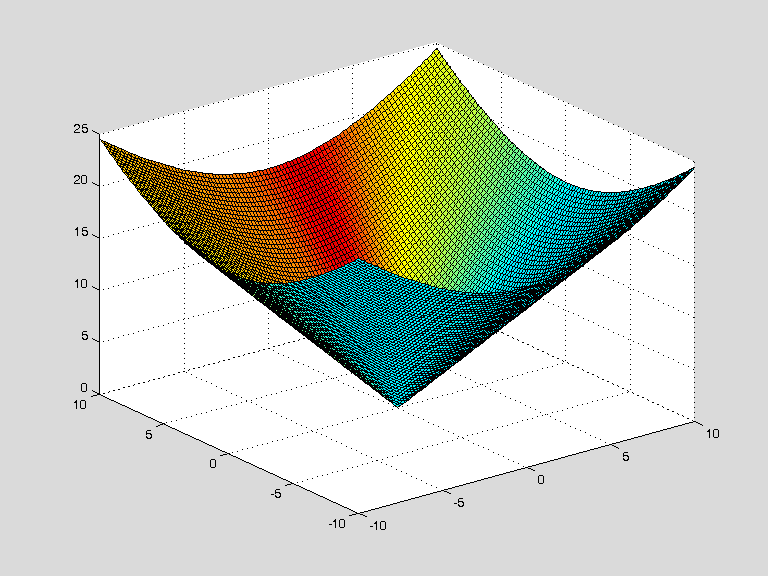
Z=sqrt(X.^2+Y.^2)/tan(pi/6);
surfl(X,Y,Z)Выводится
коническая поверхность как явная функция аппликаты от абциссы и ординаты с прямоугольной областью определения.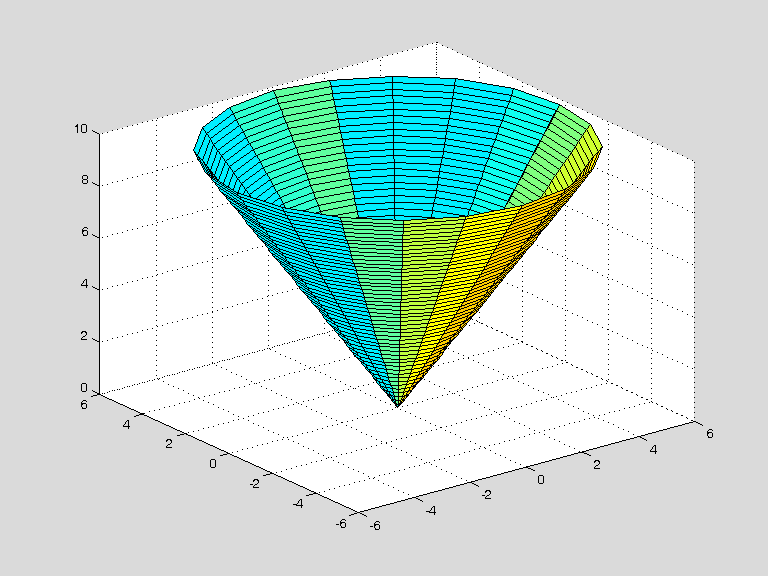
Для того,
чтобы получить
коническую поверхность
в виде
семейства окружностей
(а мы
со школы
привыкли понимать
конус именно
так), необходимо
определить ее
в цилиндрической
системе координат:
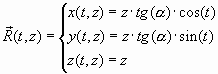 .
.
Указанные выше способы аналитического описания поверхностей подходят и для случая, когда в основании лежит эллипс. Можно также выполнять и операции переноса поверхности и поворота (аффинные преобразования). Следует отметить еще раз, что это очень частные случаи конических поверхностей.
Вернемся к
более общему
представлению конической
поверхности: 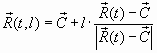 .
В качестве
направляющей рассмотрим
кривую
.
В качестве
направляющей рассмотрим
кривую 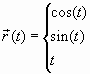 ,
, ![]() .
.
X=cx+L.*(x-cx)./sqrt((x-cx).^2+(y-cy).^2+(z-cz).^2);
Y=cy+L.*(y-cy)./sqrt((x-cx).^2+(y-cy).^2+(z-cz).^2);
Z=cz+L.*(z-cz)./sqrt((x-cx).^2+(y-cy).^2+(z-cz).^2);
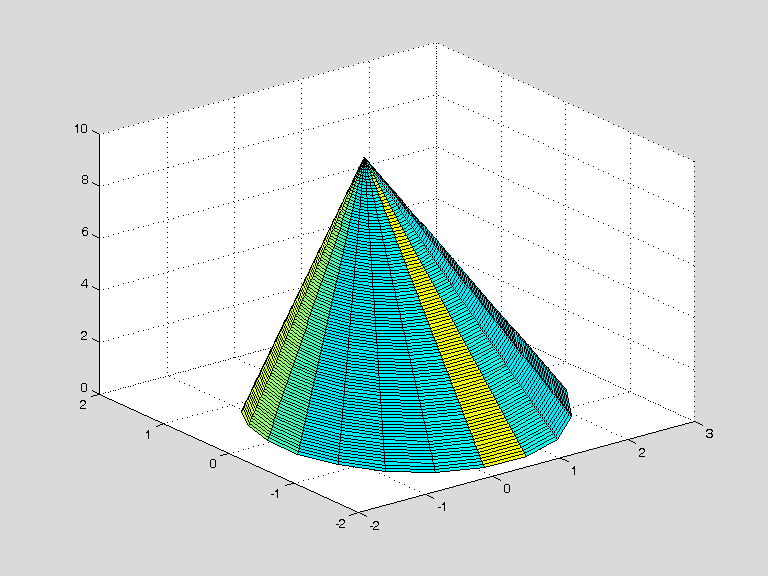
Как вариант
можно предложить
и такое
представление ![]() ,
где
,
где ![]() . В
этом случае
коническая поверхность
будет построена
от вершины
до направляющей.
. В
этом случае
коническая поверхность
будет построена
от вершины
до направляющей.
t=0:2*pi/20:2*pi;l=0:0.1:1; [T,L]=meshgrid(t,l);
x=cos(T);y=sin(T);z=T;C=[0 0 10];
cx=zeros(size(T));cx(:,:)=C(1);cy=zeros(size(T));
cy(:,:)=C(2);cz=zeros(size(T)); cz(:,:)=C(3);
X=cx+L.*(x-cx); Y=cy+L.*(y-cy); Z=cz+L.*(z-cz); surfl(X,Y,Z)